Упрощенное рассмотрение динамики движения вертолёта

Основой для вывода и использования упрощенных уравнений движения вертолёта является допущение о замене несущего винта с его сложной динамикой – равнодействующей силой. При этом предполагается, что маховое движение лопастей изменяется мгновенно при изменениях параметров движения вертолёта (скорость, угол атаки, угловая скорость) и углов общего и циклического шага лопастей.

Как правило, при таком рассмотрении не учитываются связи между продольным и боковым движениями и эти движения рассматриваются отдельно. При анализе продольного движения рассматриваются следующие уравнения:

; (2.1)

; (2.2)

; (2.3)

В уравнениях (2.1), (2.2), (2.3) учитываются только переменные и .

Входными величинами являются продольный наклон кольца автомата перекоса æ и величина общего шага φ0.

Соотношение для сил и моментов на несущем винте

Зависимости сил и моментов на несущем винте от параметров движения должны быть известны для определения параметров движения, соответствующих установившемуся режиму полета, балансировочных положений органов управления и для определения коэффициентов уравнений движения вертолета (производных устойчивости).

В практике расчетов устойчивости балансировочные отклонения управления и производные устойчивости определяются на основании данных детального аэродинамического расчета, выполняемого с помощью ЦВМ.

Основу упрощенного метода определения названных величин составляет импульсная теория несущего винта. В импульсной теории рассматривается несущий винт с постоянными углами установки лопастей по азимуту. В то же время для уравновешивания сил и моментов, действующих на вертолет, необходимо определенное введение циклического шага, зависящее от режима полета. Для получения возможности применения выводов импульсной теории к винту с переменным циклическим шагом вводится понятие эквивалентного несущего винта.

Продольная балансировка

Рассмотрим силы и моменты, действующие на вертолет в продольной плоскости (имеем ввиду одновинтовой вертолет).

На рис. 2.1 приведена схема действия упомянутых сил и моментов.

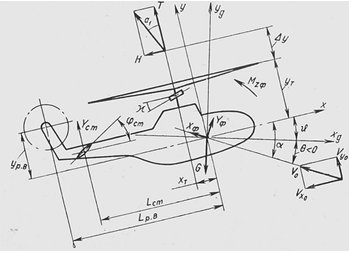
Рис. 2.1. Схема сил и моментов, действующих на вертолет в установившемся режиме полета (продольное движение).

Начало координат лежит в центре масс вертолета. Ось y связной системы координат параллельна оси несущего винта, ось x направлена вперед. Ось yg земной системы координат направлена вертикально. Как обычно, – угол тангажа вертолета; – угол атаки несущего винта и вертолета; – угол наклона траектории. Рассмотрим уравнения равновесия вертолета:

(2.4)

где X, Y, Mz – соответственно суммы сил, действующих на вертолет вдоль осей x и y и моментов относительно оси z.

В развернутом виде они равны (без учёта продольной и боковой сил и крутящего момента рулевого винта):

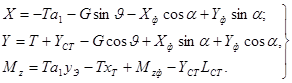(2.5)

Значение XФ может быть подсчитано по формуле

, (2.6)

где Sвр – площадь эквивалентной вредной пластинки фюзеляжа.

Величиной Yф, если вертолет не имеет крыла, можно пренебречь.

Величину продольного момента фюзеляжа можно подсчитать по формуле:

. (2.7)

Материалы о транспорте:

Технико-экономические показатели
Расчет дохода Д, руб., производится по формуле Д уч = åС+ , (35) Д уч = 673943,02+ =734597,89 где åС – общая сумма затрат на участке, руб.; % – уровень рентабельности 9 %. Расчет прибыли ...

Несущая система – кузов
Кузов автомобиля - металлический, сварной, несущей конструкции. Тип - четырехдверный седан. Все нагрузки, возникающие при движении автомобиля, воспринимает кузов, каркас которого представляет собой ж ...

Система питания
Одним из важнейших достоинств двигателя внутреннего сгорания является то, что автомобиль на одной заправке топливом может проехать 500 - 600 и более километров. Это расстояние называется запасом хода ...